Weird interview question

Some time ago, I saw interview question: given a function that produces uniformly distributed random numbers between zero and one. Calculate the Pi.

Wtf was my initial reaction. Who in the right mind would ask a question like this? But then I needed an excuse for not doing the dishes, and here we go.

My first association with Pi number is the circle area formula Pi*r^2. How can we relate our random numbers to a circle? Let say the distance between min(0) and max(1) is our radius. You can picture it like this:

The next question is how to plot our random number on 2d plane? We will call it twice. One for X and second for Y.

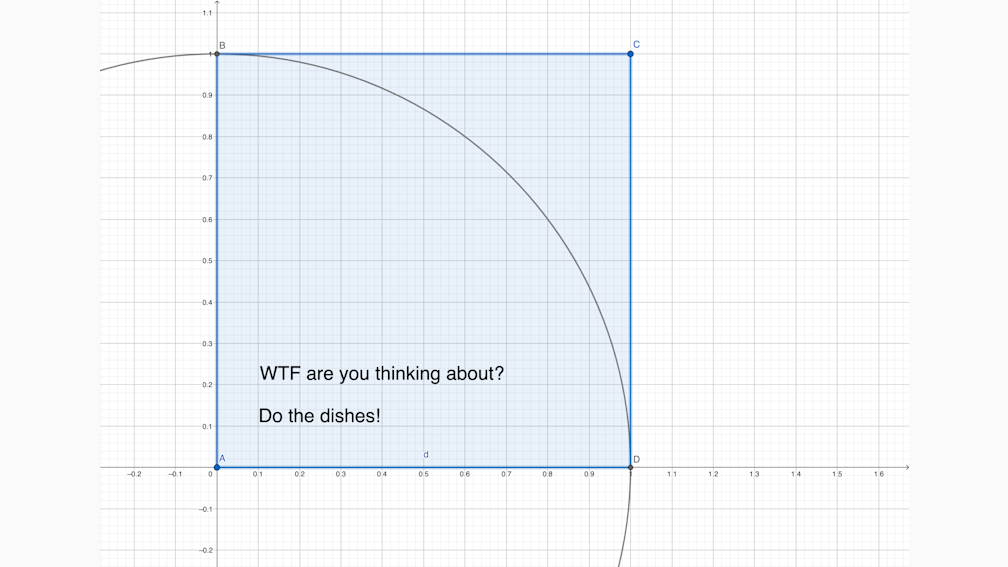
If we repeat this enough times we get a square with a side length that equals 1

Now we need to combine our circle and square.

Looking on it, Pi should be the difference between the area of a square and the area of a quarter of a circle.

It is time to dust off my math skills.

Area of a circle - Pi*r^2

Area of a quarter of a circle (QC) - (Pi*r^2)/4

four quarters equals full circle (obviously) - 4*QC = Pi*r^2

then - Pi = (4*QC)/r^2

What is r^2? It is area of a square (AS)

then - Pi = (4*QC)/AS

In English, that would be Pi equals area of e circle divided by the area of a square where the radius of a circle equals side of the square.

Now, how can we know the area of the square? Remember when we draw a square with our random dots? So count of those dots will be our area.

And the area of our quarter of a circle would be a count of dots with distance from the 0 less or equal 1. The distance formula is d = sqrt((x2-x1)^2+(y2-y1)^2).

But since we want distance from 0,0 we can simplify that to d = sqrt(x^2+y^2).

Where x and y are the coordinates of our random dot.

It is time to write some code.

I would not recommend using this method to calculate Pi for something serious. First. How to say it lightly. The accuracy of this method is not the best on the market. And second, to get stable accuracy to the second digit, you need 10 000 000 dots. So yeah, performance-wise, it is not the best method either. But it was fun.

Now I don't have any excuses left.